Let  be an acute-angled triangle, and let
be an acute-angled triangle, and let  be the circumcircle of triangle
be the circumcircle of triangle  .
.
The tangent to the circle at the point
at the point  meets the tangent to the circle
meets the tangent to the circle  at
at  at the point
at the point 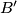 . The line
. The line 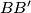 intersects the line
intersects the line  at
at  , and
, and  is the midpoint of the segment
is the midpoint of the segment  .
.
Similarly, the tangent to the circle at the point
at the point  meets the tangent to the circle
meets the tangent to the circle  at the point
at the point  at the point
at the point 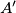 . The line
. The line 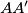 intersects the line
intersects the line  at
at  , and
, and  is the midpoint of the segment
is the midpoint of the segment  .
.
a) Show that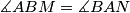 .
.
b) If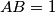 , determine the values of
, determine the values of  and
and  for the triangles
for the triangles  which maximise
which maximise 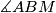 .
.
 be an acute-angled triangle, and let
be an acute-angled triangle, and let  be the circumcircle of triangle
be the circumcircle of triangle  .
. The tangent to the circle
 at the point
at the point  meets the tangent to the circle
meets the tangent to the circle  at
at  at the point
at the point 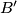 . The line
. The line 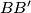 intersects the line
intersects the line  at
at  , and
, and  is the midpoint of the segment
is the midpoint of the segment  .
. Similarly, the tangent to the circle
 at the point
at the point  meets the tangent to the circle
meets the tangent to the circle  at the point
at the point  at the point
at the point 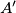 . The line
. The line 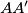 intersects the line
intersects the line  at
at  , and
, and  is the midpoint of the segment
is the midpoint of the segment  .
. a) Show that
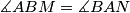 .
. b) If
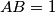 , determine the values of
, determine the values of  and
and  for the triangles
for the triangles  which maximise
which maximise 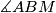 .
.  Školjka
Školjka