Determine all positive integers
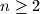
that satisfy the following condition: for all
and
relatively prime to
we have
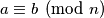
if and only if
.
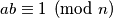
%V0
Determine all positive integers $n\geq 2$ that satisfy the following condition: for all $a$ and $b$ relatively prime to $n$ we have $a \equiv b \pmod n$ if and only if $ab\equiv 1 \pmod n$.
Školjka