Let
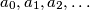
be an arbitrary infinite sequence of positive numbers. Show that the inequality
![1 + a_n > a_{n-1} \sqrt[n]{2}](/media/m/6/8/3/68300d4c59f2a509af66424e1feb09f2.png)
holds for infinitely many positive integers

.
%V0
Let $a_0, a_1, a_2, \ldots$ be an arbitrary infinite sequence of positive numbers. Show that the inequality $1 + a_n > a_{n-1} \sqrt[n]{2}$ holds for infinitely many positive integers $n$.