Let

be an acute triangle. Let
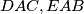
, and
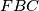
be isosceles triangles exterior to

, with
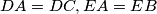
, and
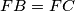
, such that
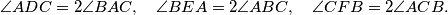
Let
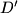
be the intersection of lines
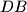
and

, let
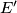
be the intersection of
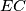
and
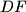
, and let
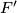
be the intersection of
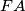
and

. Find, with proof, the value of the sum
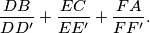
%V0
Let $ABC$ be an acute triangle. Let $DAC,EAB$, and $FBC$ be isosceles triangles exterior to $ABC$, with $DA=DC, EA=EB$, and $FB=FC$, such that
$$\angle ADC = 2\angle BAC, \quad \angle BEA= 2 \angle ABC, \quad \angle CFB = 2 \angle ACB.$$
Let $D'$ be the intersection of lines $DB$ and $EF$, let $E'$ be the intersection of $EC$ and $DF$, and let $F'$ be the intersection of $FA$ and $DE$. Find, with proof, the value of the sum
$$\frac{DB}{DD'}+\frac{EC}{EE'}+\frac{FA}{FF'}.$$