Let

be a triangle and

an exterior point in the plane of the triangle. Suppose the lines
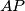
,
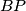
,
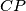
meet the sides

,

,

(or extensions thereof) in

,

,

, respectively. Suppose further that the areas of triangles
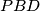
,
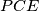
,
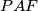
are all equal. Prove that each of these areas is equal to the area of triangle

itself.
%V0
Let $ABC$ be a triangle and $P$ an exterior point in the plane of the triangle. Suppose the lines $AP$, $BP$, $CP$ meet the sides $BC$, $CA$, $AB$ (or extensions thereof) in $D$, $E$, $F$, respectively. Suppose further that the areas of triangles $PBD$, $PCE$, $PAF$ are all equal. Prove that each of these areas is equal to the area of triangle $ABC$ itself.