Let
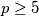
be a prime number. Prove that there exists an integer

with
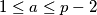
such that neither
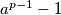
nor
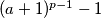
is divisible by
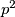
.
%V0
Let $p \geq 5$ be a prime number. Prove that there exists an integer $a$ with $1 \leq a \leq p-2$ such that neither $a^{p-1}-1$ nor $(a+1)^{p-1}-1$ is divisible by $p^2$.