Prove that there is no positive integer

such that, for
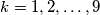
, the leftmost digit (in decimal notation) of
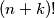
equals

.
%V0
Prove that there is no positive integer $n$ such that, for $k = 1,2,\ldots,9$, the leftmost digit (in decimal notation) of $(n+k)!$ equals $k$.