Let  be a positive integer. Each point
be a positive integer. Each point 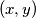 in the plane, where
in the plane, where  and
and  are non-negative integers with
are non-negative integers with 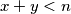 , is coloured red or blue, subject to the following condition: if a point
, is coloured red or blue, subject to the following condition: if a point 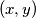 is red, then so are all points
is red, then so are all points 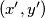 with
with 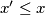 and
and 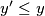 . Let
. Let  be the number of ways to choose
be the number of ways to choose  blue points with distinct
blue points with distinct  -coordinates, and let
-coordinates, and let  be the number of ways to choose
be the number of ways to choose  blue points with distinct
blue points with distinct  -coordinates. Prove that
-coordinates. Prove that 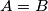 .
.
 be a positive integer. Each point
be a positive integer. Each point 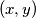 in the plane, where
in the plane, where  and
and  are non-negative integers with
are non-negative integers with 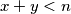 , is coloured red or blue, subject to the following condition: if a point
, is coloured red or blue, subject to the following condition: if a point 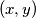 is red, then so are all points
is red, then so are all points 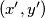 with
with 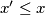 and
and 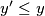 . Let
. Let  be the number of ways to choose
be the number of ways to choose  blue points with distinct
blue points with distinct  -coordinates, and let
-coordinates, and let  be the number of ways to choose
be the number of ways to choose  blue points with distinct
blue points with distinct  -coordinates. Prove that
-coordinates. Prove that 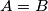 .
.  Školjka
Školjka