For any set

of five points in the plane, no three of which are collinear, let
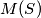
and
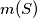
denote the greatest and smallest areas, respectively, of triangles determined by three points from

. What is the minimum possible value of
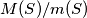
?
%V0
For any set $S$ of five points in the plane, no three of which are collinear, let $M(S)$ and $m(S)$ denote the greatest and smallest areas, respectively, of triangles determined by three points from $S$. What is the minimum possible value of $M(S)/m(S)$ ?