Let
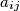
(with the indices

and

from the set
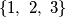
) be real numbers such that
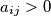
for
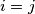
;
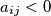
for
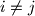
.
Prove the existence of positive real numbers
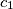
,
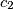
,
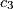
such that the numbers
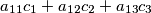
,
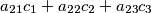
,
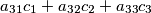
are either all negative, or all zero, or all positive.
%V0
Let $a_{ij}$ (with the indices $i$ and $j$ from the set $\left\{1,\ 2,\ 3\right\}$) be real numbers such that
$a_{ij}>0$ for $i = j$;
$a_{ij}<0$ for $i\neq j$.
Prove the existence of positive real numbers $c_{1}$, $c_{2}$, $c_{3}$ such that the numbers
$a_{11}c_{1}+a_{12}c_{2}+a_{13}c_{3}$,
$a_{21}c_{1}+a_{22}c_{2}+a_{23}c_{3}$,
$a_{31}c_{1}+a_{32}c_{2}+a_{33}c_{3}$
are either all negative, or all zero, or all positive.