Let

be a
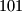
-element subset of the set
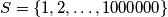
. Prove that there exist numbers
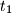
,
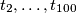
in

such that the sets
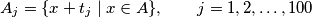
are pairwise disjoint.
%V0
Let $A$ be a $101$-element subset of the set $S=\{1,2,\ldots,1000000\}$. Prove that there exist numbers $t_1$, $t_2, \ldots, t_{100}$ in $S$ such that the sets $$A_j=\{x+t_j\mid x\in A\},\qquad j=1,2,\ldots,100$$ are pairwise disjoint.