Regard a plane with a Cartesian coordinate system; for each point with integer coordinates, draw a circular disk centered at this point and having the radius 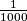 .
.
a) Prove the existence of an equilateral triangle whose vertices lie in the interior of different disks;
b) Show that every equilateral triangle whose vertices lie in the interior of different disks has a sidelength 96.
Radu Gologan, Romania
Remark
[The " 96" in (b) can be strengthened to " 124". By the way, part (a) of this problem is the place where I used the well-known "Dedekind" theorem.]
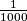 .
. a) Prove the existence of an equilateral triangle whose vertices lie in the interior of different disks;
b) Show that every equilateral triangle whose vertices lie in the interior of different disks has a sidelength 96.
Radu Gologan, Romania
Remark
[The " 96" in (b) can be strengthened to " 124". By the way, part (a) of this problem is the place where I used the well-known "Dedekind" theorem.]
 Školjka
Školjka