Given three fixed pairwisely distinct points  ,
,  ,
,  lying on one straight line in this order. Let
lying on one straight line in this order. Let  be a circle passing through
be a circle passing through  and
and  whose center does not lie on the line
whose center does not lie on the line  . The tangents to
. The tangents to  at
at  and
and  intersect each other at a point
intersect each other at a point  . The segment
. The segment 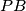 meets the circle
meets the circle  at
at  .
.
Show that the point of intersection of the angle bisector of the angle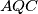 with the line
with the line  does not depend on the choice of the circle
does not depend on the choice of the circle  .
.
 ,
,  ,
,  lying on one straight line in this order. Let
lying on one straight line in this order. Let  be a circle passing through
be a circle passing through  and
and  whose center does not lie on the line
whose center does not lie on the line  . The tangents to
. The tangents to  at
at  and
and  intersect each other at a point
intersect each other at a point  . The segment
. The segment 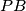 meets the circle
meets the circle  at
at  .
. Show that the point of intersection of the angle bisector of the angle
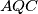 with the line
with the line  does not depend on the choice of the circle
does not depend on the choice of the circle  .
.  Školjka
Školjka