Let

be a triangle, and

a point in the interior of this triangle. Let

,

,

be the feet of the perpendiculars from the point

to the lines

,

,

, respectively. Assume that
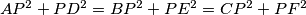
.
Furthermore, let
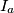
,
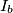
,
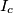
be the excenters of triangle

. Show that the point

is the circumcenter of triangle
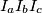
.
%V0
Let $ABC$ be a triangle, and $P$ a point in the interior of this triangle. Let $D$, $E$, $F$ be the feet of the perpendiculars from the point $P$ to the lines $BC$, $CA$, $AB$, respectively. Assume that
$AP^{2}+PD^{2}=BP^{2}+PE^{2}=CP^{2}+PF^{2}$.
Furthermore, let $I_{a}$, $I_{b}$, $I_{c}$ be the excenters of triangle $ABC$. Show that the point $P$ is the circumcenter of triangle $I_{a}I_{b}I_{c}$.