Let
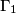
,
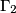
,
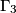
,
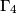
be distinct circles such that
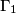
,
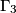
are externally tangent at

, and
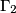
,
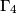
are externally tangent at the same point

. Suppose that
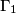
and
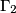
;
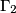
and
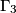
;
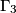
and
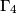
;
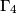
and
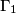
meet at

,

,

,

, respectively, and that all these points are different from

. Prove that
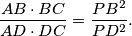
%V0
Let $\Gamma_1$, $\Gamma_2$, $\Gamma_3$, $\Gamma_4$ be distinct circles such that $\Gamma_1$, $\Gamma_3$ are externally tangent at $P$, and $\Gamma_2$, $\Gamma_4$ are externally tangent at the same point $P$. Suppose that $\Gamma_1$ and $\Gamma_2$; $\Gamma_2$ and $\Gamma_3$; $\Gamma_3$ and $\Gamma_4$; $\Gamma_4$ and $\Gamma_1$ meet at $A$, $B$, $C$, $D$, respectively, and that all these points are different from $P$. Prove that
$$\frac{AB\cdot BC}{AD\cdot DC}=\frac{PB^2}{PD^2}.$$