Each pair of opposite sides of a convex hexagon has the following property: the distance between their midpoints is equal to
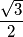
times the sum of their lengths. Prove that all the angles of the hexagon are equal.
%V0
Each pair of opposite sides of a convex hexagon has the following property: the distance between their midpoints is equal to $\dfrac{\sqrt{3}}{2}$ times the sum of their lengths. Prove that all the angles of the hexagon are equal.