The sequence 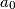 ,
,  ,
, 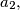
 is defined as follows:
is defined as follows: 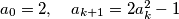 for
for 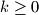 . Prove that if an odd prime
. Prove that if an odd prime  divides
divides  , then
, then 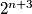 divides
divides 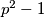 .
.
comment
Hi guys ,
Here is a nice problem:
Let be given a sequence such that
such that 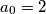 and
and 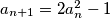 . Show that if
. Show that if  is an odd prime such that
is an odd prime such that 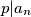 then we have
then we have 
Here are some futher question proposed by me :Prove or disprove that :
1)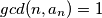
2) for every odd prime number we have
we have 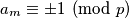 where
where 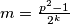 where
where 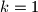 or
or 
Thanks kiu si u
Edited by Orl.
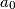 ,
,  ,
, 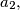
 is defined as follows:
is defined as follows: 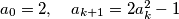 for
for 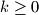 . Prove that if an odd prime
. Prove that if an odd prime  divides
divides  , then
, then 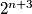 divides
divides 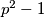 .
. comment
Hi guys ,
Here is a nice problem:
Let be given a sequence
 such that
such that 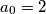 and
and 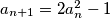 . Show that if
. Show that if  is an odd prime such that
is an odd prime such that 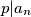 then we have
then we have 
Here are some futher question proposed by me :Prove or disprove that :
1)
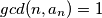
2) for every odd prime number
 we have
we have 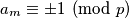 where
where 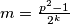 where
where 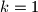 or
or 
Thanks kiu si u
Edited by Orl.
 Školjka
Školjka