The sequence 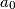 ,
,  ,
, 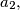
 is defined as follows:
is defined as follows: 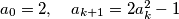 for
for 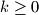 . Prove that if an odd prime
. Prove that if an odd prime  divides
divides  , then
, then 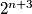 divides
divides 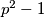 .
.
comment
Hi guys ,
Here is a nice problem:
Let be given a sequence such that
such that 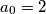 and
and 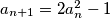 . Show that if
. Show that if  is an odd prime such that
is an odd prime such that 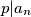 then we have
then we have 
Here are some futher question proposed by me :Prove or disprove that :
1)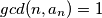
2) for every odd prime number we have
we have 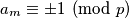 where
where 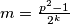 where
where 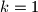 or
or 
Thanks kiu si u
Edited by Orl.
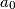 ,
,  ,
, 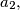
 is defined as follows:
is defined as follows: 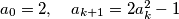 for
for 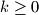 . Prove that if an odd prime
. Prove that if an odd prime  divides
divides  , then
, then 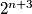 divides
divides 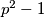 .
. comment
Hi guys ,
Here is a nice problem:
Let be given a sequence
 such that
such that 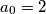 and
and 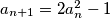 . Show that if
. Show that if  is an odd prime such that
is an odd prime such that 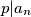 then we have
then we have 
Here are some futher question proposed by me :Prove or disprove that :
1)
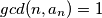
2) for every odd prime number
 we have
we have 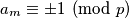 where
where 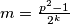 where
where 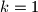 or
or 
Thanks kiu si u
Edited by Orl.
Slični zadaci
Let  be a prime number and let
be a prime number and let  be a set of positive integers that satisfies the following conditions: (1) the set of prime divisors of the elements in
be a set of positive integers that satisfies the following conditions: (1) the set of prime divisors of the elements in  consists of
consists of 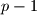 elements; (2) for any nonempty subset of
elements; (2) for any nonempty subset of  , the product of its elements is not a perfect
, the product of its elements is not a perfect  -th power. What is the largest possible number of elements in
-th power. What is the largest possible number of elements in  ?
?
 be a prime number and let
be a prime number and let  be a set of positive integers that satisfies the following conditions: (1) the set of prime divisors of the elements in
be a set of positive integers that satisfies the following conditions: (1) the set of prime divisors of the elements in  consists of
consists of 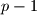 elements; (2) for any nonempty subset of
elements; (2) for any nonempty subset of  , the product of its elements is not a perfect
, the product of its elements is not a perfect  -th power. What is the largest possible number of elements in
-th power. What is the largest possible number of elements in  ?
?  Školjka
Školjka  and
and  be distinct integers greater than
be distinct integers greater than  . Prove that there exists a positive integer
. Prove that there exists a positive integer  such that
such that 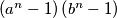 is not a perfect square.
is not a perfect square. be a positive integer. Show that if there exists a sequence
be a positive integer. Show that if there exists a sequence 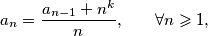 then
then 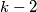 is divisible by
is divisible by  .
. is not the square of an integer. Determine all integers
is not the square of an integer. Determine all integers  with the following property:
with the following property: 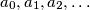 be an increasing sequence of nonnegative integers such that every nonnegative integer can be expressed uniquely in the form
be an increasing sequence of nonnegative integers such that every nonnegative integer can be expressed uniquely in the form 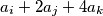 , where
, where 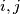 and
and 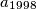 .
. 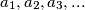 as follows.
as follows. 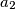 are coprime positive integers and
are coprime positive integers and 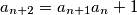 . Show that for every
. Show that for every 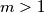 there is an
there is an 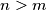 such that
such that 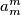 divides
divides 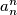 . Is it true that
. Is it true that 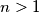 ?
?