Let  be a prime number and let
be a prime number and let  be a set of positive integers that satisfies the following conditions: (1) the set of prime divisors of the elements in
be a set of positive integers that satisfies the following conditions: (1) the set of prime divisors of the elements in  consists of
consists of 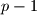 elements; (2) for any nonempty subset of
elements; (2) for any nonempty subset of  , the product of its elements is not a perfect
, the product of its elements is not a perfect  -th power. What is the largest possible number of elements in
-th power. What is the largest possible number of elements in  ?
?
 be a prime number and let
be a prime number and let  be a set of positive integers that satisfies the following conditions: (1) the set of prime divisors of the elements in
be a set of positive integers that satisfies the following conditions: (1) the set of prime divisors of the elements in  consists of
consists of 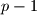 elements; (2) for any nonempty subset of
elements; (2) for any nonempty subset of  , the product of its elements is not a perfect
, the product of its elements is not a perfect  -th power. What is the largest possible number of elements in
-th power. What is the largest possible number of elements in  ?
?  Školjka
Školjka