Let
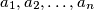
be positive real numbers,
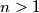
. Denote by
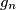
their geometric mean, and by
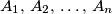
the sequence of arithmetic means defined by
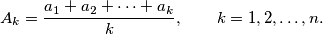
Let
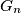
be the geometric mean of
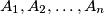
. Prove the inequality
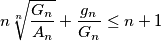
and establish the cases of equality.
%V0
Let ${a_1,a_2,\dots,a_n}$ be positive real numbers, ${n>1}$. Denote by $g_n$ their geometric mean, and by $A_1,\,A_2,\,\dots,\,A_n$ the sequence of arithmetic means defined by
$$A_k=\frac{a_1+a_2+\cdots+a_k}{k},\qquad k=1,2,\dots,n.$$
Let $G_n$ be the geometric mean of $A_1,A_2,\dots,A_n$. Prove the inequality $$n \root n\of{\frac{G_n}{A_n}}+ \frac{g_n}{G_n}\le n+1 $$ and establish the cases of equality.