Consider a matrix of size 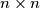 whose entries are real numbers of absolute value not exceeding
whose entries are real numbers of absolute value not exceeding  . The sum of all entries of the matrix is
. The sum of all entries of the matrix is  . Let
. Let  be an even positive integer. Determine the least number
be an even positive integer. Determine the least number  such that every such matrix necessarily has a row or a column with the sum of its entries not exceeding
such that every such matrix necessarily has a row or a column with the sum of its entries not exceeding  in absolute value.
in absolute value.
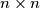 whose entries are real numbers of absolute value not exceeding
whose entries are real numbers of absolute value not exceeding  . The sum of all entries of the matrix is
. The sum of all entries of the matrix is  . Let
. Let  be an even positive integer. Determine the least number
be an even positive integer. Determine the least number  such that every such matrix necessarily has a row or a column with the sum of its entries not exceeding
such that every such matrix necessarily has a row or a column with the sum of its entries not exceeding  in absolute value.
in absolute value.  Školjka
Školjka