Let 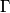 be a circle and let
be a circle and let  be a line such that
be a line such that 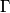 and
and  have no common points. Further, let
have no common points. Further, let  be a diameter of the circle
be a diameter of the circle 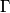 ; assume that this diameter
; assume that this diameter  is perpendicular to the line
is perpendicular to the line  , and the point
, and the point  is nearer to the line
is nearer to the line  than the point
than the point  . Let
. Let  be an arbitrary point on the circle
be an arbitrary point on the circle 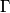 , different from the points
, different from the points  and
and  . Let
. Let  be the point of intersection of the lines
be the point of intersection of the lines  and
and  . One of the two tangents from the point
. One of the two tangents from the point  to the circle
to the circle 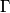 touches this circle
touches this circle 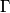 at a point
at a point  ; hereby, we assume that the points
; hereby, we assume that the points  and
and  lie in the same halfplane with respect to the line
lie in the same halfplane with respect to the line  . Denote by
. Denote by  the point of intersection of the lines
the point of intersection of the lines 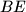 and
and  . Let the line
. Let the line 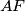 intersect the circle
intersect the circle 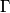 at a point
at a point 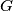 , different from
, different from  .
.
Prove that the reflection of the point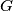 in the line
in the line  lies on the line
lies on the line 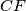 .
.
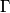 be a circle and let
be a circle and let  be a line such that
be a line such that 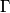 and
and  have no common points. Further, let
have no common points. Further, let  be a diameter of the circle
be a diameter of the circle 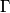 ; assume that this diameter
; assume that this diameter  is perpendicular to the line
is perpendicular to the line  , and the point
, and the point  is nearer to the line
is nearer to the line  than the point
than the point  . Let
. Let  be an arbitrary point on the circle
be an arbitrary point on the circle 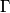 , different from the points
, different from the points  and
and  . Let
. Let  be the point of intersection of the lines
be the point of intersection of the lines  and
and  . One of the two tangents from the point
. One of the two tangents from the point  to the circle
to the circle 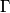 touches this circle
touches this circle 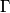 at a point
at a point  ; hereby, we assume that the points
; hereby, we assume that the points  and
and  lie in the same halfplane with respect to the line
lie in the same halfplane with respect to the line  . Denote by
. Denote by  the point of intersection of the lines
the point of intersection of the lines 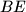 and
and  . Let the line
. Let the line 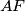 intersect the circle
intersect the circle 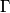 at a point
at a point 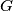 , different from
, different from  .
. Prove that the reflection of the point
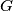 in the line
in the line  lies on the line
lies on the line 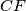 .
.  Školjka
Školjka