Let  be an acute-angled triangle such that
be an acute-angled triangle such that 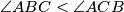 , let
, let  be the circumcenter of triangle
be the circumcenter of triangle  , and let
, and let 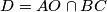 . Denote by
. Denote by  and
and  the circumcenters of triangles
the circumcenters of triangles 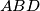 and
and 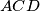 , respectively. Let
, respectively. Let  be a point on the extension of the segment
be a point on the extension of the segment  beyound
beyound  such that
such that 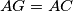 , and let
, and let  be a point on the extension of the segment
be a point on the extension of the segment  beyound
beyound  such that
such that 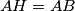 . Prove that the quadrilateral
. Prove that the quadrilateral 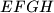 is a rectangle if and only if
is a rectangle if and only if 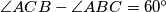 .
.
comment
Official version Let be the circumcenter of an acute-angled triangle
be the circumcenter of an acute-angled triangle  with
with 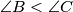 . The line
. The line 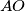 meets the side
meets the side  at
at  . The circumcenters of the triangles
. The circumcenters of the triangles 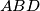 and
and 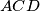 are
are  and
and  , respectively. Extend the sides
, respectively. Extend the sides 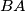 and
and  beyond
beyond  , and choose on the respective extensions points
, and choose on the respective extensions points  and
and  such that
such that 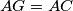 and
and 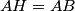 . Prove that the quadrilateral
. Prove that the quadrilateral 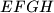 is a rectangle if and only if
is a rectangle if and only if 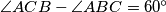 .
.
Edited by orl.
 be an acute-angled triangle such that
be an acute-angled triangle such that 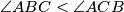 , let
, let  be the circumcenter of triangle
be the circumcenter of triangle  , and let
, and let 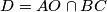 . Denote by
. Denote by  and
and  the circumcenters of triangles
the circumcenters of triangles 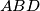 and
and 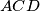 , respectively. Let
, respectively. Let  be a point on the extension of the segment
be a point on the extension of the segment  beyound
beyound  such that
such that 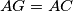 , and let
, and let  be a point on the extension of the segment
be a point on the extension of the segment  beyound
beyound  such that
such that 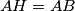 . Prove that the quadrilateral
. Prove that the quadrilateral 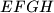 is a rectangle if and only if
is a rectangle if and only if 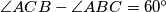 .
. comment
Official version Let
 be the circumcenter of an acute-angled triangle
be the circumcenter of an acute-angled triangle  with
with 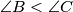 . The line
. The line 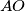 meets the side
meets the side  at
at  . The circumcenters of the triangles
. The circumcenters of the triangles 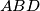 and
and 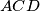 are
are  and
and  , respectively. Extend the sides
, respectively. Extend the sides 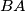 and
and  beyond
beyond  , and choose on the respective extensions points
, and choose on the respective extensions points  and
and  such that
such that 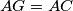 and
and 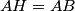 . Prove that the quadrilateral
. Prove that the quadrilateral 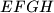 is a rectangle if and only if
is a rectangle if and only if 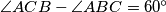 .
.Edited by orl.
 Školjka
Školjka