Let 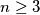 be a fixed integer. Each side and each diagonal of a regular
be a fixed integer. Each side and each diagonal of a regular  -gon is labelled with a number from the set
-gon is labelled with a number from the set 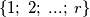 in a way such that the following two conditions are fulfilled:
in a way such that the following two conditions are fulfilled:
1. Each number from the set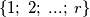 occurs at least once as a label.
occurs at least once as a label.
2. In each triangle formed by three vertices of the -gon, two of the sides are labelled with the same number, and this number is greater than the label of the third side.
-gon, two of the sides are labelled with the same number, and this number is greater than the label of the third side.
(a) Find the maximal for which such a labelling is possible.
for which such a labelling is possible.
(b) Harder version (IMO Shortlist 2005): For this maximal value of , how many such labellings are there?
, how many such labellings are there?
Easier version (5th German TST 2006) - contains answer to the harder versionEasier version (5th German TST 2006): Show that, for this maximal value of , there are exactly
, there are exactly 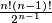 possible labellings.
possible labellings.
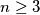 be a fixed integer. Each side and each diagonal of a regular
be a fixed integer. Each side and each diagonal of a regular  -gon is labelled with a number from the set
-gon is labelled with a number from the set 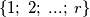 in a way such that the following two conditions are fulfilled:
in a way such that the following two conditions are fulfilled: 1. Each number from the set
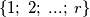 occurs at least once as a label.
occurs at least once as a label. 2. In each triangle formed by three vertices of the
 -gon, two of the sides are labelled with the same number, and this number is greater than the label of the third side.
-gon, two of the sides are labelled with the same number, and this number is greater than the label of the third side. (a) Find the maximal
 for which such a labelling is possible.
for which such a labelling is possible. (b) Harder version (IMO Shortlist 2005): For this maximal value of
 , how many such labellings are there?
, how many such labellings are there? Easier version (5th German TST 2006) - contains answer to the harder versionEasier version (5th German TST 2006): Show that, for this maximal value of
 , there are exactly
, there are exactly 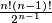 possible labellings.
possible labellings.  Školjka
Školjka