Suppose that

,
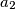
,

,

are integers such that
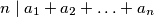
.
Prove that there exist two permutations
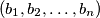
and
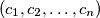
of
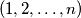
such that for each integer

with
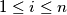
, we have
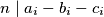
%V0
Suppose that $a_1$, $a_2$, $\ldots$, $a_n$ are integers such that $n\mid a_1 + a_2 + \ldots + a_n$.
Prove that there exist two permutations $\left(b_1,b_2,\ldots,b_n\right)$ and $\left(c_1,c_2,\ldots,c_n\right)$ of $\left(1,2,\ldots,n\right)$ such that for each integer $i$ with $1\leq i\leq n$, we have
$$n\mid a_i - b_i - c_i$$