Suppose we have a  -gon. Some
-gon. Some 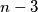 diagonals are coloured black and some other
diagonals are coloured black and some other 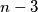 diagonals are coloured red (a side is not a diagonal), so that no two diagonals of the same colour can intersect strictly inside the polygon, although they can share a vertex. Find the maximum number of intersection points between diagonals coloured differently strictly inside the polygon, in terms of
diagonals are coloured red (a side is not a diagonal), so that no two diagonals of the same colour can intersect strictly inside the polygon, although they can share a vertex. Find the maximum number of intersection points between diagonals coloured differently strictly inside the polygon, in terms of  .
.
 -gon. Some
-gon. Some 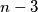 diagonals are coloured black and some other
diagonals are coloured black and some other 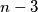 diagonals are coloured red (a side is not a diagonal), so that no two diagonals of the same colour can intersect strictly inside the polygon, although they can share a vertex. Find the maximum number of intersection points between diagonals coloured differently strictly inside the polygon, in terms of
diagonals are coloured red (a side is not a diagonal), so that no two diagonals of the same colour can intersect strictly inside the polygon, although they can share a vertex. Find the maximum number of intersection points between diagonals coloured differently strictly inside the polygon, in terms of  .
.  Školjka
Školjka