Let
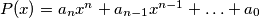
, where
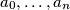
are integers,
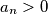
,
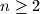
. Prove that there exists a positive integer

such that
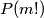
is a composite number.
%V0
Let $P(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+\ldots+a_{0}$, where $a_{0},\ldots,a_{n}$ are integers, $a_{n}>0$, $n\geq 2$. Prove that there exists a positive integer $m$ such that $P(m!)$ is a composite number.