The sequence 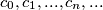 is defined by
is defined by 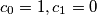 , and
, and 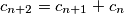 for
for 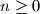 . Consider the set
. Consider the set  of ordered pairs
of ordered pairs 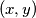 for which there is a finite set
for which there is a finite set 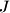 of positive integers such that
of positive integers such that 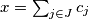 ,
, 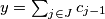 . Prove that there exist real numbers
. Prove that there exist real numbers 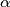 ,
, 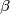 , and
, and  with the following property: An ordered pair of nonnegative integers
with the following property: An ordered pair of nonnegative integers 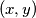 satisfies the inequality
satisfies the inequality 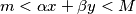 if and only if
if and only if 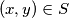 .
.
Remark: A sum over the elements of the empty set is assumed to be .
.
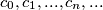 is defined by
is defined by 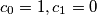 , and
, and 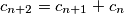 for
for 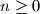 . Consider the set
. Consider the set  of ordered pairs
of ordered pairs 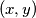 for which there is a finite set
for which there is a finite set 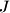 of positive integers such that
of positive integers such that 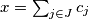 ,
, 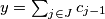 . Prove that there exist real numbers
. Prove that there exist real numbers 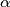 ,
, 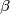 , and
, and  with the following property: An ordered pair of nonnegative integers
with the following property: An ordered pair of nonnegative integers 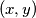 satisfies the inequality
satisfies the inequality 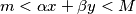 if and only if
if and only if 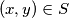 .
. Remark: A sum over the elements of the empty set is assumed to be
 .
.  Školjka
Školjka