Let  be a finite set of points in the plane such that no three of them are on a line. For each convex polygon
be a finite set of points in the plane such that no three of them are on a line. For each convex polygon  whose vertices are in
whose vertices are in  , let
, let 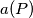 be the number of vertices of
be the number of vertices of  , and let
, and let 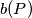 be the number of points of
be the number of points of  which are outside
which are outside  . A line segment, a point, and the empty set are considered as convex polygons of
. A line segment, a point, and the empty set are considered as convex polygons of  ,
,  , and
, and  vertices respectively. Prove that for every real number
vertices respectively. Prove that for every real number  :
:
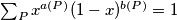 , where the sum is taken over all convex polygons with vertices in
, where the sum is taken over all convex polygons with vertices in  .
.
Alternative formulation:
Let be a finite point set in the plane and no three points are collinear. A subset
be a finite point set in the plane and no three points are collinear. A subset  of
of  will be called round if its elements is the set of vertices of a convex
will be called round if its elements is the set of vertices of a convex 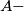 gon
gon 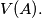 For each round subset let
For each round subset let 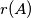 be the number of points from
be the number of points from  which are exterior from the convex
which are exterior from the convex 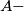 gon
gon 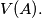 Subsets with
Subsets with 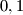 and 2 elements are always round, its corresponding polygons are the empty set, a point or a segment, respectively (for which all other points that are not vertices of the polygon are exterior). For each round subset
and 2 elements are always round, its corresponding polygons are the empty set, a point or a segment, respectively (for which all other points that are not vertices of the polygon are exterior). For each round subset  of
of  construct the polynomial
construct the polynomial
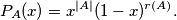
Show that the sum of polynomials for all round subsets is exactly the polynomial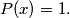
 be a finite set of points in the plane such that no three of them are on a line. For each convex polygon
be a finite set of points in the plane such that no three of them are on a line. For each convex polygon  whose vertices are in
whose vertices are in  , let
, let 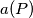 be the number of vertices of
be the number of vertices of  , and let
, and let 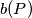 be the number of points of
be the number of points of  which are outside
which are outside  . A line segment, a point, and the empty set are considered as convex polygons of
. A line segment, a point, and the empty set are considered as convex polygons of  ,
,  , and
, and  vertices respectively. Prove that for every real number
vertices respectively. Prove that for every real number  :
: 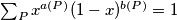 , where the sum is taken over all convex polygons with vertices in
, where the sum is taken over all convex polygons with vertices in  .
. Alternative formulation:
Let
 be a finite point set in the plane and no three points are collinear. A subset
be a finite point set in the plane and no three points are collinear. A subset  of
of  will be called round if its elements is the set of vertices of a convex
will be called round if its elements is the set of vertices of a convex 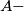 gon
gon  For each round subset let
For each round subset let 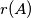 be the number of points from
be the number of points from  which are exterior from the convex
which are exterior from the convex 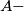 gon
gon 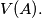 Subsets with
Subsets with 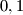 and 2 elements are always round, its corresponding polygons are the empty set, a point or a segment, respectively (for which all other points that are not vertices of the polygon are exterior). For each round subset
and 2 elements are always round, its corresponding polygons are the empty set, a point or a segment, respectively (for which all other points that are not vertices of the polygon are exterior). For each round subset  of
of  construct the polynomial
construct the polynomial 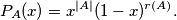
Show that the sum of polynomials for all round subsets is exactly the polynomial
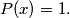
 Školjka
Školjka