A holey triangle is an upward equilateral triangle of side length  with
with  upward unit triangular holes cut out. A diamond is a
upward unit triangular holes cut out. A diamond is a 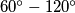 unit rhombus.
unit rhombus.
Prove that a holey triangle can be tiled with diamonds if and only if the following condition holds: Every upward equilateral triangle of side length
can be tiled with diamonds if and only if the following condition holds: Every upward equilateral triangle of side length  in
in  contains at most
contains at most  holes, for
holes, for 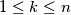 .
.
 with
with  upward unit triangular holes cut out. A diamond is a
upward unit triangular holes cut out. A diamond is a 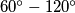 unit rhombus.
unit rhombus. Prove that a holey triangle
 can be tiled with diamonds if and only if the following condition holds: Every upward equilateral triangle of side length
can be tiled with diamonds if and only if the following condition holds: Every upward equilateral triangle of side length  in
in  contains at most
contains at most  holes, for
holes, for 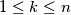 .
. Slični zadaci
Let the sides  and
and  of the quadrilateral
of the quadrilateral  (such that
(such that  is not parallel to
is not parallel to  ) intersect at point
) intersect at point  . Points
. Points 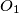 and
and 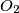 are circumcenters and points
are circumcenters and points 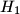 and
and 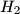 are orthocenters of triangles
are orthocenters of triangles 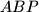 and
and 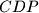 , respectively. Denote the midpoints of segments
, respectively. Denote the midpoints of segments 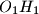 and
and 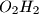 by
by 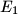 and
and 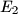 , respectively. Prove that the perpendicular from
, respectively. Prove that the perpendicular from 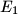 on
on  , the perpendicular from
, the perpendicular from 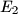 on
on  and the lines
and the lines 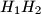 are concurrent.
are concurrent.
Proposed by Ukraine
 and
and  of the quadrilateral
of the quadrilateral  (such that
(such that  is not parallel to
is not parallel to  ) intersect at point
) intersect at point  . Points
. Points 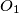 and
and 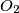 are circumcenters and points
are circumcenters and points 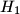 and
and 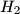 are orthocenters of triangles
are orthocenters of triangles 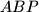 and
and 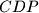 , respectively. Denote the midpoints of segments
, respectively. Denote the midpoints of segments 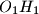 and
and 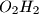 by
by 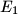 and
and 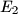 , respectively. Prove that the perpendicular from
, respectively. Prove that the perpendicular from 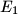 on
on  , the perpendicular from
, the perpendicular from 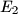 on
on  and the lines
and the lines 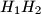 are concurrent.
are concurrent.Proposed by Ukraine
Determine the smallest positive real number  with the following property. Let
with the following property. Let  be a convex quadrilateral, and let points
be a convex quadrilateral, and let points  ,
,  ,
,  , and
, and 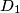 lie on sides
lie on sides  ,
,  ,
,  , and
, and 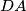 , respectively. Consider the areas of triangles
, respectively. Consider the areas of triangles 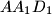 ,
, 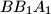 ,
, 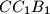 and
and 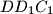 ; let
; let  be the sum of the two smallest ones, and let
be the sum of the two smallest ones, and let  be the area of quadrilateral
be the area of quadrilateral 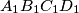 . Then we always have
. Then we always have 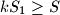 .
.
Author: unknown author, USA
 with the following property. Let
with the following property. Let  be a convex quadrilateral, and let points
be a convex quadrilateral, and let points  ,
,  ,
,  , and
, and 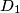 lie on sides
lie on sides  ,
,  ,
,  , and
, and 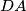 , respectively. Consider the areas of triangles
, respectively. Consider the areas of triangles 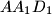 ,
, 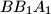 ,
, 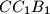 and
and 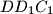 ; let
; let  be the sum of the two smallest ones, and let
be the sum of the two smallest ones, and let  be the area of quadrilateral
be the area of quadrilateral 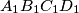 . Then we always have
. Then we always have 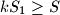 .
. Author: unknown author, USA
 Školjka
Školjka 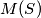 and
and 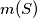 denote the greatest and smallest areas, respectively, of triangles determined by three points from
denote the greatest and smallest areas, respectively, of triangles determined by three points from 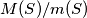 ?
?  be a triangle and
be a triangle and 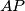 ,
, 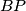 ,
, 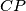 meet the sides
meet the sides  ,
,  ,
,  ,
,  , respectively. Suppose further that the areas of triangles
, respectively. Suppose further that the areas of triangles 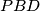 ,
, 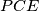 ,
, 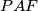 are all equal. Prove that each of these areas is equal to the area of triangle
are all equal. Prove that each of these areas is equal to the area of triangle 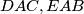 , and
, and 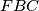 be isosceles triangles exterior to
be isosceles triangles exterior to 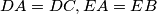 , and
, and 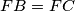 , such that
, such that 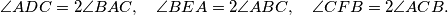
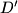 be the intersection of lines
be the intersection of lines 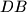 and
and  , let
, let 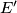 be the intersection of
be the intersection of 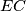 and
and 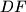 , and let
, and let 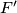 be the intersection of
be the intersection of 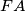 and
and 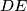 . Find, with proof, the value of the sum
. Find, with proof, the value of the sum 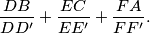
 its orthocenter,
its orthocenter,  its circumcenter, and
its circumcenter, and  its circumradius. Let
its circumradius. Let  across the line
across the line  across the line
across the line  across the line
across the line 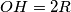 .
.