Let
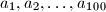
be nonnegative real numbers such that
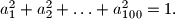
Prove that
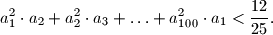
Author: Marcin Kuzma, Poland
%V0
Let $a_1, a_2, \ldots, a_{100}$ be nonnegative real numbers such that $a^2_1 + a^2_2 + \ldots + a^2_{100} = 1.$ Prove that
$$a^2_1 \cdot a_2 + a^2_2 \cdot a_3 + \ldots + a^2_{100} \cdot a_1 < \frac {12}{25}.$$
Author: Marcin Kuzma, Poland