Given is a convex polygon

with

vertices. Triangle whose vertices lie on vertices of

is called good if all its sides are equal in length. Prove that there are at most
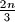
good triangles.
Author: unknown author, Ukraine
%V0
Given is a convex polygon $P$ with $n$ vertices. Triangle whose vertices lie on vertices of $P$ is called good if all its sides are equal in length. Prove that there are at most $\frac {2n}{3}$ good triangles.
Author: unknown author, Ukraine