Determine the smallest positive real number  with the following property. Let
with the following property. Let  be a convex quadrilateral, and let points
be a convex quadrilateral, and let points 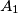 ,
, 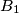 ,
, 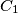 , and
, and 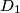 lie on sides
lie on sides  ,
,  ,
,  , and
, and  , respectively. Consider the areas of triangles
, respectively. Consider the areas of triangles 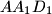 ,
, 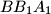 ,
, 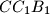 and
and 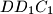 ; let
; let  be the sum of the two smallest ones, and let
be the sum of the two smallest ones, and let 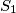 be the area of quadrilateral
be the area of quadrilateral 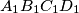 . Then we always have
. Then we always have 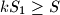 .
.
Author: unknown author, USA
 with the following property. Let
with the following property. Let  be a convex quadrilateral, and let points
be a convex quadrilateral, and let points 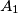 ,
, 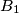 ,
, 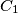 , and
, and 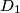 lie on sides
lie on sides  ,
,  ,
,  , and
, and  , respectively. Consider the areas of triangles
, respectively. Consider the areas of triangles 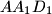 ,
, 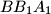 ,
, 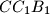 and
and 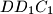 ; let
; let  be the sum of the two smallest ones, and let
be the sum of the two smallest ones, and let 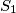 be the area of quadrilateral
be the area of quadrilateral 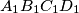 . Then we always have
. Then we always have 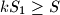 .
. Author: unknown author, USA
 Školjka
Školjka