Let
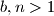
be integers. Suppose that for each

there exists an integer
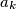
such that
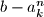
is divisible by
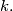
Prove that
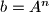
for some integer
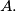
Author: unknown author, Canada
%V0
Let $b,n > 1$ be integers. Suppose that for each $k > 1$ there exists an integer $a_k$ such that $b - a^n_k$ is divisible by $k.$ Prove that $b = A^n$ for some integer $A.$
Author: unknown author, Canada