Slični zadaci
A positive integer  is called balanced, if
is called balanced, if 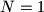 or if
or if  can be written as a product of an even number of not necessarily distinct primes. Given positive integers
can be written as a product of an even number of not necessarily distinct primes. Given positive integers  and
and  , consider the polynomial
, consider the polynomial  defined by
defined by 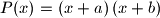 .
.
a) Prove that there exist distinct positive integers and
and  such that all the number
such that all the number 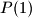 ,
, 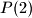 , ...,
, ..., 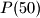 are balanced.
are balanced.
b) Prove that if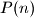 is balanced for all positive integers
is balanced for all positive integers  , then
, then 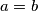 .
.
Proposed by Jorge Tipe, Peru
 is called balanced, if
is called balanced, if 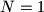 or if
or if  can be written as a product of an even number of not necessarily distinct primes. Given positive integers
can be written as a product of an even number of not necessarily distinct primes. Given positive integers  and
and  , consider the polynomial
, consider the polynomial  defined by
defined by 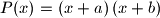 .
.a) Prove that there exist distinct positive integers
 and
and  such that all the number
such that all the number 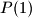 ,
, 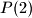 , ...,
, ..., 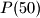 are balanced.
are balanced.b) Prove that if
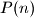 is balanced for all positive integers
is balanced for all positive integers  , then
, then 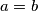 .
.Proposed by Jorge Tipe, Peru
 Školjka
Školjka 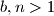 be integers. Suppose that for each
be integers. Suppose that for each  there exists an integer
there exists an integer 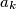 such that
such that 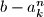 is divisible by
is divisible by 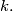 Prove that
Prove that 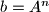 for some integer
for some integer 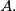
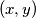 of positive integers satisfying the equation
of positive integers satisfying the equation 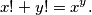
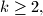 prove that
prove that 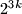 divides the number
divides the number 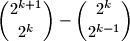
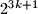 does not.
does not. 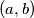 such that
such that  divides
divides 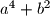 .
.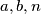 be positive integers,
be positive integers, 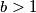 and
and 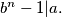 Show that the representation of the number
Show that the representation of the number 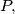 if, for all
if, for all 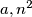 divides
divides 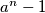 whenever
whenever