Let
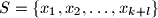
be a
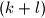
-element set of real numbers contained in the interval
![[0, 1]](/media/m/7/f/0/7f04c41d91b0555ac792351e836cbd4e.png)
;

and
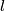
are positive integers. A

-element subset
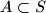
is called nice if
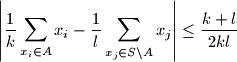
Prove that the number of nice subsets is at least
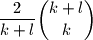
.
Proposed by Andrey Badzyan, Russia
%V0
Let $S = \{x_1, x_2, \ldots, x_{k + l}\}$ be a $(k + l)$-element set of real numbers contained in the interval $[0, 1]$; $k$ and $l$ are positive integers. A $k$-element subset $A\subset S$ is called nice if
$$\left |\frac {1}{k}\sum_{x_i\in A} x_i - \frac {1}{l}\sum_{x_j\in S\setminus A} x_j\right |\le \frac {k + l}{2kl}$$
Prove that the number of nice subsets is at least $\dfrac{2}{k + l}\dbinom{k + l}{k}$.
Proposed by Andrey Badzyan, Russia