In an acute triangle

segments

and
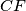
are altitudes. Two circles passing through the point

anf

and tangent to the line

at the points

and

so that

lies between

and

. Prove that lines
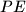
and
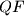
intersect on the circumcircle of triangle
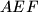
.
Proposed by Davood Vakili, Iran
%V0
In an acute triangle $ABC$ segments $BE$ and $CF$ are altitudes. Two circles passing through the point $A$ anf $F$ and tangent to the line $BC$ at the points $P$ and $Q$ so that $B$ lies between $C$ and $Q$. Prove that lines $PE$ and $QF$ intersect on the circumcircle of triangle $AEF$.
Proposed by Davood Vakili, Iran