Let  and
and  be integers with
be integers with 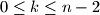 . Consider a set
. Consider a set  of
of  lines in the plane such that no two of them are parallel and no three have a common point. Denote by
lines in the plane such that no two of them are parallel and no three have a common point. Denote by  the set of intersections of lines in
the set of intersections of lines in  . Let
. Let 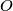 be a point in the plane not lying on any line of
be a point in the plane not lying on any line of  . A point
. A point 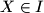 is colored red if the open line segment
is colored red if the open line segment 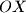 intersects at most
intersects at most  lines in
lines in  . Prove that
. Prove that  contains at least
contains at least 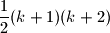 red points.
red points.
Proposed by Gerhard Woeginger, Netherlands
 and
and  be integers with
be integers with 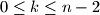 . Consider a set
. Consider a set  of
of  lines in the plane such that no two of them are parallel and no three have a common point. Denote by
lines in the plane such that no two of them are parallel and no three have a common point. Denote by  the set of intersections of lines in
the set of intersections of lines in  . Let
. Let 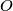 be a point in the plane not lying on any line of
be a point in the plane not lying on any line of  . A point
. A point 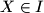 is colored red if the open line segment
is colored red if the open line segment 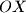 intersects at most
intersects at most  lines in
lines in  . Prove that
. Prove that  contains at least
contains at least 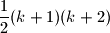 red points.
red points. Proposed by Gerhard Woeginger, Netherlands
 Školjka
Školjka