There is given a convex quadrilateral

. Prove that there exists a point

inside the quadrilateral such that
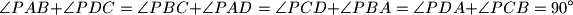
if and only if the diagonals

and
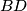
are perpendicular.
Proposed by Dukan Dukic, Serbia
%V0
There is given a convex quadrilateral $ABCD$. Prove that there exists a point $P$ inside the quadrilateral such that
$$\angle PAB + \angle PDC = \angle PBC + \angle PAD = \angle PCD + \angle PBA = \angle PDA + \angle PCB = 90^{\circ}$$
if and only if the diagonals $AC$ and $BD$ are perpendicular.
Proposed by Dukan Dukic, Serbia