Let
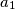
,
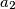
,

,
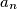
be distinct positive integers,
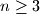
. Prove that there exist distinct indices

and
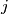
such that
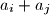
does not divide any of the numbers
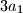
,
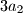
,

,
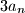
.
Proposed by Mohsen Jamaali, Iran
%V0
Let $a_1$, $a_2$, $\ldots$, $a_n$ be distinct positive integers, $n\ge 3$. Prove that there exist distinct indices $i$ and $j$ such that $a_i + a_j$ does not divide any of the numbers $3a_1$, $3a_2$, $\ldots$, $3a_n$.
Proposed by Mohsen Jamaali, Iran