Let
be a positive integer. Show that the numbers
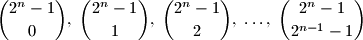
are congruent modulo
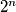
to
,
,
,
,
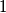
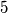
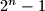
in some order.
Proposed by Duskan Dukic, Serbia
%V0
Let $n$ be a positive integer. Show that the numbers
$$\binom{2^n - 1}{0},\; \binom{2^n - 1}{1},\; \binom{2^n - 1}{2},\; \ldots,\; \binom{2^n - 1}{2^{n - 1} - 1}$$
are congruent modulo $2^n$ to $1$, $3$, $5$, $\ldots$, $2^n - 1$ in some order.
Proposed by Duskan Dukic, Serbia
Školjka