Find all functions

from the set of real numbers into the set of real numbers which satisfy for all

,

the identity
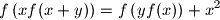
Proposed by Japan
%V0
Find all functions $f$ from the set of real numbers into the set of real numbers which satisfy for all $x$, $y$ the identity $$f\left(xf(x+y)\right) = f\left(yf(x)\right) +x^2$$
Proposed by Japan