Let

be a polygon that is convex and symmetric to some point
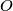
. Prove that for some parallelogram
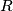
satisfying

we have
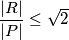
where
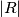
and
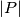
denote the area of the sets
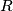
and

, respectively.
Proposed by Witold Szczechla, Poland
%V0
Let $P$ be a polygon that is convex and symmetric to some point $O$. Prove that for some parallelogram $R$ satisfying $P\subset R$ we have $$\frac{|R|}{|P|}\leq \sqrt 2$$ where $|R|$ and $|P|$ denote the area of the sets $R$ and $P$, respectively.
Proposed by Witold Szczechla, Poland