Let the sides  and
and  of the quadrilateral
of the quadrilateral  (such that
(such that  is not parallel to
is not parallel to  ) intersect at point
) intersect at point  . Points
. Points 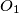 and
and 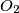 are circumcenters and points
are circumcenters and points 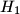 and
and 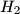 are orthocenters of triangles
are orthocenters of triangles 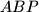 and
and 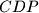 , respectively. Denote the midpoints of segments
, respectively. Denote the midpoints of segments 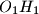 and
and 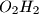 by
by 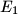 and
and 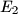 , respectively. Prove that the perpendicular from
, respectively. Prove that the perpendicular from 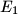 on
on  , the perpendicular from
, the perpendicular from 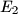 on
on  and the lines
and the lines 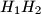 are concurrent.
are concurrent.
Proposed by Ukraine
 and
and  of the quadrilateral
of the quadrilateral  (such that
(such that  is not parallel to
is not parallel to  ) intersect at point
) intersect at point  . Points
. Points 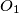 and
and 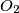 are circumcenters and points
are circumcenters and points 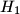 and
and 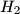 are orthocenters of triangles
are orthocenters of triangles 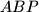 and
and 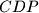 , respectively. Denote the midpoints of segments
, respectively. Denote the midpoints of segments 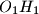 and
and 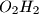 by
by 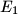 and
and 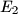 , respectively. Prove that the perpendicular from
, respectively. Prove that the perpendicular from 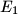 on
on  , the perpendicular from
, the perpendicular from 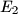 on
on  and the lines
and the lines 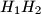 are concurrent.
are concurrent.Proposed by Ukraine
 Školjka
Školjka