Let

be a circumscribed quadrilateral. Let

be a line through

which meets the segment

in

and the line

in

. Denote by
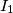
,
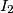
and
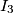
the incenters of
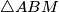
,
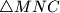
and
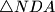
, respectively. Prove that the orthocenter of
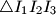
lies on

.
Proposed by Nikolay Beluhov, Bulgaria
%V0
Let $ABCD$ be a circumscribed quadrilateral. Let $g$ be a line through $A$ which meets the segment $BC$ in $M$ and the line $CD$ in $N$. Denote by $I_1$, $I_2$ and $I_3$ the incenters of $\triangle ABM$, $\triangle MNC$ and $\triangle NDA$, respectively. Prove that the orthocenter of $\triangle I_1I_2I_3$ lies on $g$.
Proposed by Nikolay Beluhov, Bulgaria