A positive integer  is called balanced, if
is called balanced, if 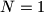 or if
or if  can be written as a product of an even number of not necessarily distinct primes. Given positive integers
can be written as a product of an even number of not necessarily distinct primes. Given positive integers  and
and  , consider the polynomial
, consider the polynomial  defined by
defined by 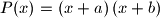 .
.
a) Prove that there exist distinct positive integers and
and  such that all the number
such that all the number 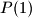 ,
, 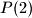 , ...,
, ..., 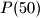 are balanced.
are balanced.
b) Prove that if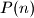 is balanced for all positive integers
is balanced for all positive integers  , then
, then 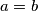 .
.
Proposed by Jorge Tipe, Peru
 is called balanced, if
is called balanced, if 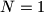 or if
or if  can be written as a product of an even number of not necessarily distinct primes. Given positive integers
can be written as a product of an even number of not necessarily distinct primes. Given positive integers  and
and  , consider the polynomial
, consider the polynomial  defined by
defined by 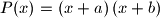 .
.a) Prove that there exist distinct positive integers
 and
and  such that all the number
such that all the number 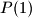 ,
, 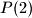 , ...,
, ..., 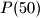 are balanced.
are balanced.b) Prove that if
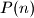 is balanced for all positive integers
is balanced for all positive integers  , then
, then 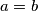 .
.Proposed by Jorge Tipe, Peru
 Školjka
Školjka