Let

be a non-constant function from the set of positive integers into the set of positive integer, such that

divides
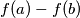
for all distinct positive integers

,

. Prove that there exist infinitely many primes

such that

divides
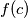
for some positive integer

.
Proposed by Juhan Aru, Estonia
%V0
Let $f$ be a non-constant function from the set of positive integers into the set of positive integer, such that $a-b$ divides $f\!\left(a\right)-f\!\left(b\right)$ for all distinct positive integers $a$, $b$. Prove that there exist infinitely many primes $p$ such that $p$ divides $f\!\left(c\right)$ for some positive integer $c$.
Proposed by Juhan Aru, Estonia