Let

and

be distinct integers greater than

. Prove that there exists a positive integer

such that
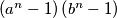
is not a perfect square.
Proposed by Mongolia
%V0
Let $a$ and $b$ be distinct integers greater than $1$. Prove that there exists a positive integer $n$ such that $\left(a^n-1\right)\left(b^n-1\right)$ is not a perfect square.
Proposed by Mongolia