Prosti
Kvaliteta:
Avg: 4,0Težina:
Avg: 5,5 Neka je skup prirodnih brojeva podijeljen u intervale na sljedeći način:
U prvom intervalu je broj 1, u drugom brojevi 2 i 3, u trećem 4, 5 i 6 i u svakom idućem jedan broj više nego u prethodnom (brojevi u intervalima su uzastopni).
Neka je udio prostih brojeva u
udio prostih brojeva u  -tom intervalu.
-tom intervalu.
a) Dokaži ili opovrgni: Postoji beskonačno brojeva za koje je
za koje je 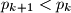 .
.
b) Dokaži ili opovrgni: Postoji beskonačno brojeva za koje je
za koje je 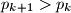 .
.
U prvom intervalu je broj 1, u drugom brojevi 2 i 3, u trećem 4, 5 i 6 i u svakom idućem jedan broj više nego u prethodnom (brojevi u intervalima su uzastopni).
Neka je
 udio prostih brojeva u
udio prostih brojeva u  -tom intervalu.
-tom intervalu.a) Dokaži ili opovrgni: Postoji beskonačno brojeva
 za koje je
za koje je 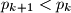 .
.b) Dokaži ili opovrgni: Postoji beskonačno brojeva
 za koje je
za koje je 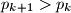 .
. Izvor: Originalan (valjda???)
Komentari:
vux, 23. travnja 2012. 19:05
grga, 21. travnja 2012. 21:55
borna, mozes li napisati kako si ti zamislio rjesenje?
nemojte ovo citati ako zelite jos rjesavat zadatak jer ima mali spoiler
takoder, sta mislite o ovom:
isti zadatak, samo je pitanje postoji li podjela prirodnih brojeva na beskonacno intervala ( ne nuzno rastucih ili neogranicenih ), npr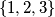 ,
, 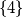 ,
, 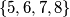 , ..., tako da
, ..., tako da  i
i  ne vrijede?
ne vrijede?
vjerojatno nema neko elegantno rjesenje al eto..
imam dojam da je nemoguce napravit podjelu u kojoj bi se udio prostih povecavao, al da se smanjuje to mi se cak i cini moguce.
nemojte ovo citati ako zelite jos rjesavat zadatak jer ima mali spoiler
takoder, sta mislite o ovom:
isti zadatak, samo je pitanje postoji li podjela prirodnih brojeva na beskonacno intervala ( ne nuzno rastucih ili neogranicenih ), npr
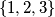 ,
, 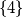 ,
, 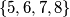 , ..., tako da
, ..., tako da  i
i  ne vrijede?
ne vrijede?vjerojatno nema neko elegantno rjesenje al eto..
imam dojam da je nemoguce napravit podjelu u kojoj bi se udio prostih povecavao, al da se smanjuje to mi se cak i cini moguce.
Zadnja promjena: grga, 21. travnja 2012. 21:56
grga, 20. travnja 2012. 19:19
dcevid, 19. travnja 2012. 14:03
vux, 16. travnja 2012. 19:21
pbakic, 16. travnja 2012. 19:20
To bi bilo skroz ok... pogotovo što će možda probudit još malo volje za radom u onima koji su na rubu predaje :D
mislim da bi bilo pametno staviti (da stavim) neko upozorenje u slucaju da ides otvoriti rjesenje zadatka koji nisi rijesio (a pogotovo ako je na To Do). skoro sam sada procitao bakicevo rjesenje -.-
sto kazete?
sto kazete?
ikicic, 16. travnja 2012. 18:51
Filip_Wee, 16. travnja 2012. 18:05
Filip_Wee, 16. travnja 2012. 18:04
pbakic, 16. travnja 2012. 18:03
vux, 16. travnja 2012. 18:02
pbakic, 16. travnja 2012. 18:01
Filip_Wee, 16. travnja 2012. 17:42
yup
http://www.google.hr/imgres?q=i+don%27t+know+what+i%27m+doing+meme&um=1&hl=hr&sa=N&biw=1920&bih=1099&tbm=isch&tbnid=k16XQqbPnvY9JM:&imgrefurl=http://imgur.com/gallery/zvl5Z&docid=ocuov7foyjN1rM&imgurl=http://chzscience.files.wordpress.com/2011/11/funny-science-news-experiments-memes-dog-science-fuzzy-logic.jpg&w=500&h=282&ei=cz-MT-ycGq_P4QSYpZSSCg&zoom=1&iact=rc&dur=252&sig=103608042134443889841&page=1&tbnh=79&tbnw=140&start=0&ndsp=65&ved=1t:429,r:2,s:0,i:66&tx=81&ty=24
http://www.google.hr/imgres?q=i+don%27t+know+what+i%27m+doing+meme&um=1&hl=hr&sa=N&biw=1920&bih=1099&tbm=isch&tbnid=k16XQqbPnvY9JM:&imgrefurl=http://imgur.com/gallery/zvl5Z&docid=ocuov7foyjN1rM&imgurl=http://chzscience.files.wordpress.com/2011/11/funny-science-news-experiments-memes-dog-science-fuzzy-logic.jpg&w=500&h=282&ei=cz-MT-ycGq_P4QSYpZSSCg&zoom=1&iact=rc&dur=252&sig=103608042134443889841&page=1&tbnh=79&tbnw=140&start=0&ndsp=65&ved=1t:429,r:2,s:0,i:66&tx=81&ty=24
Zadnja promjena: Filip_Wee, 16. travnja 2012. 17:49
pbakic, 16. travnja 2012. 17:42
pbakic, 16. travnja 2012. 17:22
 Školjka
Školjka 

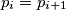
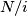
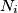 broj prostih u
broj prostih u 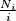 ili jednostavno
ili jednostavno