grga, 23. travnja 2012. 20:31
u dva se nemoze, za
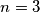
uzmi
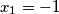
,
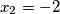
,
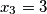
,
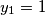
,
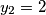
,
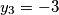
stovise, za ovu trojku se nemoze ni iz jednakosti

,

,
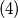
,
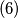
, ...
bas zato sta je
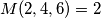
, pa mi se cini kao da ti te dodatne jednakosti ne trebaju. tako da, cini mi se da bi za
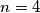
mogao postojat protuprimjer za
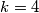
, al ga nemogu naci.
%V0
u dva se nemoze, za $n=3$
uzmi $x_1 = -1$, $x_2 = -2$, $x_3 = 3$, $y_1 = 1$, $y_2 = 2$, $y_3 = -3$
stovise, za ovu trojku se nemoze ni iz jednakosti $(1)$, $(2)$, $(4)$, $(6)$, ...
bas zato sta je $M(2, 4, 6) = 2$, pa mi se cini kao da ti te dodatne jednakosti ne trebaju. tako da, cini mi se da bi za $n=4$ mogao postojat protuprimjer za $k=4$, al ga nemogu naci.
vux, 23. travnja 2012. 19:40
nisam još pokušavao, al oko 90% sam da se može u n, a oko 30% da se može u 2
edit:nikako se ne može u 2
%V0
nisam još pokušavao, al oko 90% sam da se može u n, a oko 30% da se može u 2
edit:nikako se ne može u 2
Zadnja promjena:
vux, 23. travnja 2012. 20:15
grga, 22. travnja 2012. 15:36
sad sam malo izmjenio onaj uvjet da su svi rel prosti. al, malo mi se cini los zadatak. jesi ziher da je dobro za
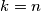
.. meni se zapravo cini da je minimalni
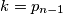
, tj
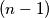
-vi prosti broj.
%V0
sad sam malo izmjenio onaj uvjet da su svi rel prosti. al, malo mi se cini los zadatak. jesi ziher da je dobro za $k = n$.. meni se zapravo cini da je minimalni $k = p_{n-1}$, tj $(n-1)$-vi prosti broj.
vux, 22. travnja 2012. 00:19
uzmi u 1. dijelu da su xi nultočke P(x), a yi nultočke Q(x), raspisivanjem ovih jednadžbi (množit ih i slično) mislim da možeš dobit da se za k=n se koeficijenti podudaraju, pa time i iksevi i ipsiloni, al nisam još siguran kaj za k<n, na trenutak mi se čak učinilo da je k=2 rješenje...
%V0
uzmi u 1. dijelu da su xi nultočke P(x), a yi nultočke Q(x), raspisivanjem ovih jednadžbi (množit ih i slično) mislim da možeš dobit da se za k=n se koeficijenti podudaraju, pa time i iksevi i ipsiloni, al nisam još siguran kaj za k<n, na trenutak mi se čak učinilo da je k=2 rješenje...
grga, 21. travnja 2012. 19:35
tj neznam dal ima rjesenje uopce, nisam uspio rijesit u nekom kracem vremenu.
%V0
tj neznam dal ima rjesenje uopce, nisam uspio rijesit u nekom kracem vremenu.
grga, 21. travnja 2012. 18:36
neznam ako ovo ima neko normalno rjesenje. prvi dio valjda ima.
%V0
neznam ako ovo ima neko normalno rjesenje. prvi dio valjda ima.
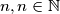 , te
, te 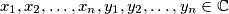
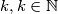 , takav da se iz jednakosti
, takav da se iz jednakosti 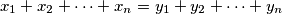
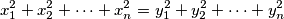

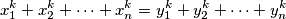
 -evi" do na permutaciju jednaki "
-evi" do na permutaciju jednaki " -ima". ako postoji, koji je najmanji takav
-ima". ako postoji, koji je najmanji takav  .
.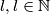 takav da se za proizvoljnih
takav da se za proizvoljnih  brojeva
brojeva 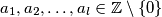 , takvih da
, takvih da 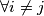 vrijedi
vrijedi 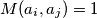 te odgovarajucih jednakosti
te odgovarajucih jednakosti 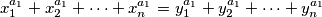
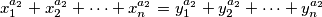

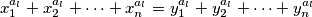
 -evi" do na permutaciju jednaki "
-evi" do na permutaciju jednaki " -ima". ako postoji, koji je najmanji takav
-ima". ako postoji, koji je najmanji takav  .
.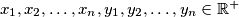 , smijemo li uzeti
, smijemo li uzeti 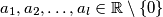 ?
? 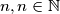 , te
, te 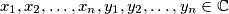
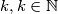 , takav da se iz jednakosti
, takav da se iz jednakosti 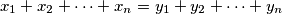
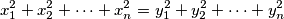

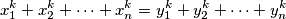
 -evi" do na permutaciju jednaki "
-evi" do na permutaciju jednaki " -ima". ako postoji, koji je najmanji takav
-ima". ako postoji, koji je najmanji takav  .
.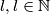 takav da se za proizvoljnih
takav da se za proizvoljnih  brojeva
brojeva 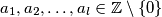 , takvih da
, takvih da 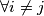 vrijedi
vrijedi 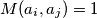 te odgovarajucih jednakosti
te odgovarajucih jednakosti 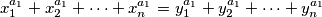
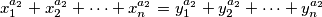

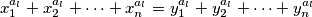
 -evi" do na permutaciju jednaki "
-evi" do na permutaciju jednaki " -ima". ako postoji, koji je najmanji takav
-ima". ako postoji, koji je najmanji takav  .
.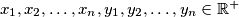 , smijemo li uzeti
, smijemo li uzeti 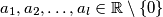 ?
?  Školjka
Školjka 

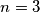
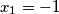 ,
, 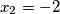 ,
, 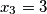 ,
, 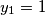 ,
, 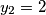 ,
, 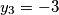
 ,
,  ,
, 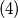 ,
, 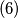 , ...
, ...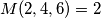 , pa mi se cini kao da ti te dodatne jednakosti ne trebaju. tako da, cini mi se da bi za
, pa mi se cini kao da ti te dodatne jednakosti ne trebaju. tako da, cini mi se da bi za 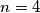 mogao postojat protuprimjer za
mogao postojat protuprimjer za 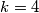 , al ga nemogu naci.
, al ga nemogu naci. 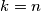 .. meni se zapravo cini da je minimalni
.. meni se zapravo cini da je minimalni 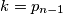 , tj
, tj 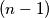 -vi prosti broj.
-vi prosti broj.